Cálculo de materiales
Volumen total de superadobe
Al calcular el volumen de superadobe se obtienen las longitudes necesarias de saco y alambre, así como el volumen de material de drenaje.
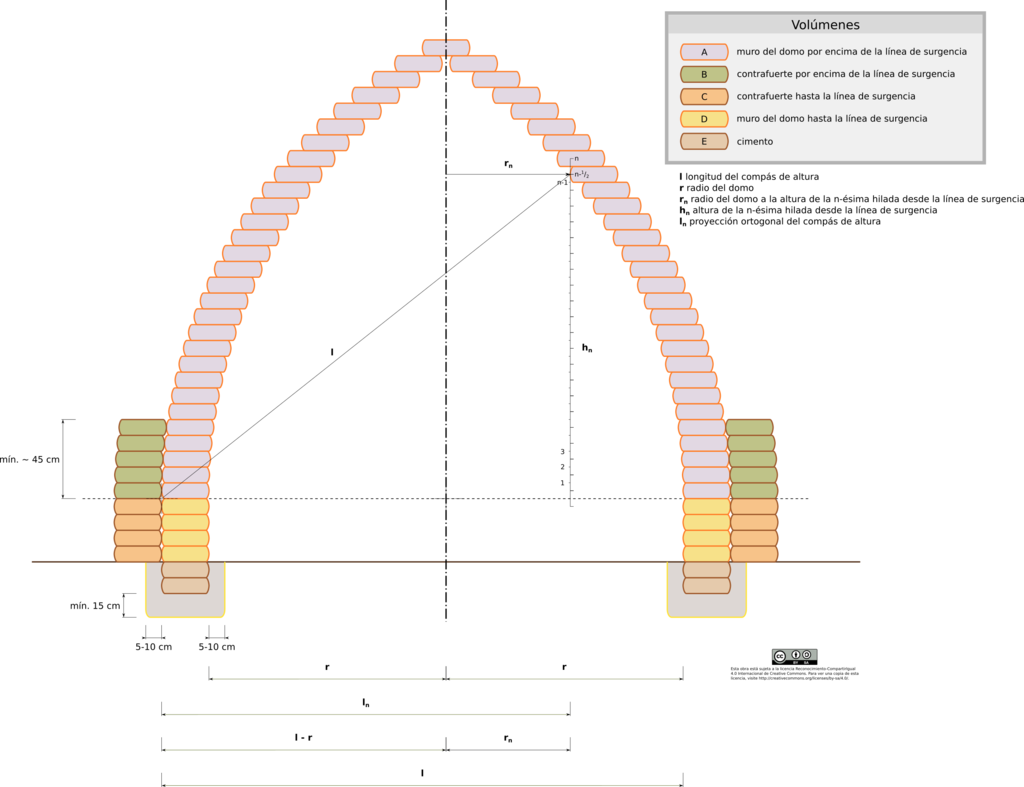
Para el cálculo del volumen de superadobe, se calcula la longitud de cada hilada —longitud de la circunferencia que describe el tubo— en el punto medio del saco —por similitud con el cálculo del volumen de un toro— y se multiplica por la sección del saco lleno y compactado. En cada hilada, la longitud de la circunferencia es función del radio del domo a la altura del saco. Por debajo de la línea de surgencia el radio es constante.
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_A} volumen de superadobe por encima de la línea de surgencia
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle N \text{ — número de hiladas por encima de la línea de surgencia}}
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{l}^2 = h^2+(\color{Green}{l}-\color{Green}{r})^2 \\ h=\sqrt{\color{Green}{l}^2 - \left(\color{Green}{l} - \color{Green}{r} \right)^2} \\ N = \dfrac{h}{\color{Green}{s_h}} \\ N = \dfrac{ \sqrt{ \color{Green}{l}^2 - \left(\color{Green}{l} - \color{Green}{r} \right)^2 } }{\color{Green}{s_h}} }
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_A(n) & = A_{saco} \\ & =\color{Green}{s_w} \color{Green}{s_h} 2 \pi r_{n(A)} \\ & = \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left(\color{Green}{r} - \color{Green}{l} + \frac{1}{2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right) \end{align} }
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_A & = \color{Green}{s_w} \color{Green}{s_h} 2 \pi \sum_{n=1}^N \left(\color{Green}{r} - \color{Green}{l} + \frac{1}{2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right) \\ & = \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left[ N \left(\color{Green}{r} - \color{Green}{l} + \frac{1}{2}\color{Green}{s_w} \right) + \sum_{n=1}^N \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right] \end{align} }
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_B} volumen de superadobe en el contrafuerte por encima de la línea de surgencia
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{h_c} \text{ — altura del contrafuerte por encima de la línea de surgencia (m)} \\ C \text{ — número de hiladas del contrafuerte por encima de la línea de surgencia} \\ C = \dfrac{\color{Green}{h_c}}{\color{Green}{s_h}} }
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_B(n) & = \color{Green}{s_w} \color{Green}{s_h} 2 \pi r_{n(B)} \\ & = \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left(\color{Green}{r} - \color{Green}{l} + \frac{3}{2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right) \end{align} }
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_B & = \color{Green}{s_w} \color{Green}{s_h} 2 \pi \sum_{n=1}^C \left(\color{Green}{r} - \color{Green}{l} + \frac{3}{2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right) \\ & = \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left[ C \left(\color{Green}{r} - \color{Green}{l} + \frac{3}{2}\color{Green}{s_w} \right) + \sum_{n=1}^C \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right] \end{align} }
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_C} volumen de superadobe en el contrafuerte por debajo de la línea de surgencia
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{n_C} \text{ — número de hiladas hasta la línea de surgencia del contrafuerte}}
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_C & = \color{Green}{n_c}(\color{Green}{s_w} \color{Green}{s_h})(2 \pi r_c) \\ & = \color{Green}{n_c} \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left(\color{Green}{r} + \frac{3}{2} \color{Green}{s_w} \right) \end{align} }
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_D} volumen de superadobe por debajo de la línea de surgencia
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{n_D} \text{ — número de hiladas hasta la línea de surgencia}}
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_D & = \color{Green}{n_D}(\color{Green}{s_w} \color{Green}{s_h})(2 \pi r_D) \\ & = \color{Green}{n_D} \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) \end{align} }
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_E} volumen de superadobe en los cimientos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{n_E} \text{ — número de hiladas en los cimientos}}
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_E & = \color{Green}{n_E}(\color{Green}{s_w} \color{Green}{s_h})(2 \pi r_E) \\ & = \color{Green}{n_E} \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) \end{align} }
Ecuaciones
Sección del saco
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{L_v} \text{— anchura del saco vacío} \\ \color{Green}{s_h} — \text{altura del saco lleno y compactado} \\ s_w — \text{anchura del saco lleno y compactado} }
Sección rectangular

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle s_w = \color{Green}{L_v} - \color{Green}{s_h} \\ A_{saco} = s_w \times \color{Green}{s_h} = \left(\color{Green}{L_v} - \color{Green}{s_h} \right) \times \color{Green}{s_h}}
Sección con laterales semicurculares
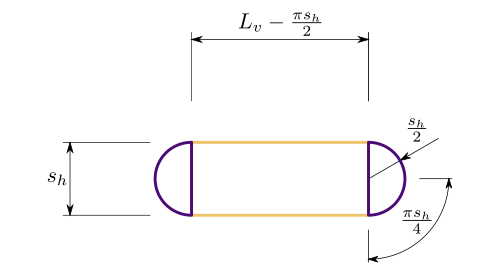
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle s_w = \color{Green}{L_v} - \dfrac{\pi \color{Green}{s_h}}{2} + \color{Green}{s_h} = \color{Green}{L_v} + \color{Green}{s_h}\left(1 - \dfrac{\pi}{2}\right) \\ A_{saco} = \left(\color{Green}{L_v} - \dfrac{\pi \color{Green}{s_h}}{2} \right) \times \color{Green}{s_h} + \pi \left(\dfrac{\color{Green}{s_h}}{2}\right)^2 = \color{Green}{L_v} \color{Green}{s_h} - \dfrac{\pi \color{Green}{s_h}^2}{4} }
Sección con laterales como segmentos circulares
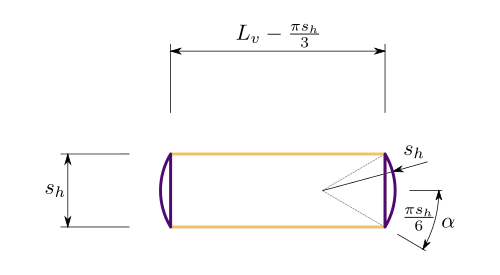
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle s_w = \color{Green}{L_v} - \dfrac{\pi \color{Green}{s_h}}{3} + 2 \left(\color{Green}{s_h} - \sqrt{\color{Green}{s_h}^2 - \left(\dfrac{\color{Green}{s_h}}{2} \right)^2} \right) = \color{Green}{L_v} - \dfrac{\pi \color{Green}{s_h}}{3} + 2 \left(\color{Green}{s_h} - \color{Green}{s_h} \dfrac{\sqrt{3}}{2} \right) = \color{Green}{L_v} + \color{Green}{s_h} \left( 2 - \dfrac{\sqrt{3}}{2} - \dfrac{\pi}{3} \right) = \color{Green}{L_v} + \dfrac{\color{Green}{s_h}}{3} \left( 6 - 3\sqrt{3} - {\pi} \right) \\ \sin \alpha = \dfrac{\dfrac{\color{Green}{s_h}}{2}}{\color{Green}{s_h}} = \dfrac{1}{2}; \alpha = 30^\circ \\ \begin{align} A_{saco} & = \left(\color{Green}{L_v} - \dfrac{\pi \color{Green}{s_h}}{3} \right) \times \color{Green}{s_h} + 2 \left(\pi \color{Green}{s_h}^2 \times \dfrac{2\alpha}{360} - \dfrac{1}{2} \times \color{Green}{s_h} \sqrt{\color{Green}{s_h}^2 - \left(\dfrac{\color{Green}{s_h}}{2} \right)^2} \right) \\ & = \color{Green}{L_v} \color{Green}{s_h} - \dfrac{\pi \color{Green}{s_h}^2}{3} + 2 \left(\pi \color{Green}{s_h}^2 \times \dfrac{1}{6} - \dfrac{1}{2} \times \dfrac{\color{Green}{s_h}^2 \sqrt{3}}{2} \right) \\ & = \color{Green}{L_v} \color{Green}{s_h} - \dfrac{\pi \color{Green}{s_h}^2}{3} + \dfrac{\pi \color{Green}{s_h}^2}{3} - \dfrac{\color{Green}{s_h}^2 \sqrt{3}}{2} \\ & = \color{Green}{L_v} \color{Green}{s_h} - \color{Green}{s_h}^2 \dfrac{\sqrt{3}}{2} \end{align} }
Sección para cálculos
Usar una sección u otra conlleva variaciones en los cálculos, ya que el área de cada una es distinta:
| Altura del saco lleno y compactado | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sección rectangular | Sección con semicírculos | Sección con segmentos circulares | ||||||||
| in | 2,00 | 3,00 | 5,00 | 2,00 | 3,00 | 5,00 | 2,00 | 3,00 | 5,00 | |
| cm | 5,08 | 7,62 | 12,70 | 5,08 | 7,62 | 12,70 | 5,08 | 7,62 | 12,70 | |
| Anchura del saco vacío (cm) | 30 | 126,59 | 170,54 | 219,71 | 132,13 | 183,00 | 254,32 | 130,05 | 178,31 | 241,32 |
| 35 | 151,99 | 208,64 | 283,21 | 157,53 | 221,10 | 317,82 | 155,45 | 216,41 | 304,82 | |
| 40 | 177,39 | 246,74 | 346,71 | 182,93 | 259,20 | 381,32 | 180,85 | 254,51 | 368,32 | |
| 45 | 202,79 | 284,84 | 410,21 | 208,33 | 297,30 | 444,82 | 206,25 | 292,61 | 431,82 | |
| 50 | 228,19 | 322,94 | 473,71 | 233,73 | 335,40 | 508,32 | 231,65 | 330,71 | 495,32 | |
| 55 | 253,59 | 361,04 | 537,21 | 259,13 | 373,50 | 571,82 | 257,05 | 368,81 | 558,82 | |
| 60 | 278,99 | 399,14 | 600,71 | 284,53 | 411,60 | 635,32 | 282,45 | 406,91 | 622,32 | |
Valores de sección
El área de la sección del saco, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle A_{saco}} , debe multiplicarse por la longitud del mismo —longitud de la circunferencia que describe el tubo en la hilada correspondiente—, que en cada caso es función del radio del domo a la altura del saco; a esta medida se suma la mitad de la anchura del saco lleno —por similitud con el cálculo del volumen de un toro—. Por debajo de la línea de surgencia el radio es constante:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle r_C = {\color{Green}{r} + {3 \over 2} s_w} \text{ — para el volumen de C} \\ r_{D,E} = {\color{Green}{r} + {1 \over 2} s_w} \text{ — para los volúmenes de D y E} }
Por encima de la línea de surgencia, el radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle r_n}
de la n-ésima hilada lo determinan la longitud del compás de altura Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle l}
y la altura donde se encuentra el saco, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle h_n}
, que, considerando la altura hasta la mitad del saco, es igual a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle n − {1 \over 2}}
veces la altura del saco lleno Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle s_h}
. Aplicando el teorema de Pitágoras:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{l}^2 = h_n^2 + l_n^2 }
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{l}^2 = h_n^2 + l_n^2 \\ l_n = \color{Green}{l} - \color{Green}{r} + r_n \\ h_n = \left(n - {1 \over 2} \right)\color{Green}{s_h} }
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{l}^2 = \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2 + \left(\color{Green}{l} -\color{Green}{r} + r_n \right)^2 \\ \color{Green}{l} -\color{Green}{r} + r_n = \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2} \\ r_n = \color{Green}{r} - \color{Green}{l} + \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2} }
Añadiendo la mitad de la anchura del saco lleno, el radio resultante para el cálculo de los volúmenes del muro del domo por encima de la línea de surgencia (volúmenes en A) es:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle r_{n(A)} = \color{Green}{r} - \color{Green}{l} + {1 \over 2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2} }
Los volúmenes de B se calculan añadiendo a la fórmula anterior la anchura del saco lleno:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle r_{n(B)} = \color{Green}{r} - \color{Green}{l} + {3 \over 2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2} }
Con las fórmulas anteriores, la suma de volúmenes queda como sigue:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V = \sum_{x=A}^{E} V_x = V_A + V_B + V_C + V_C + V_E}
Volumen total de superadobe
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V & = \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left[ N \left(\color{Green}{r} - \color{Green}{l} + \frac{1}{2}\color{Green}{s_w} \right) + \sum_{n=1}^N \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right] + \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left[ C \left(\color{Green}{r} - \color{Green}{l} + \frac{3}{2}\color{Green}{s_w} \right) + \sum_{n=1}^C \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right] + \color{Green}{n_C} \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left(\color{Green}{r} + \frac{3}{2} \color{Green}{s_w} \right) + \color{Green}{n_D} \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) + \color{Green}{n_E} \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) \\ & = \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left[ \left(N + C \right) \left(\color{Green}{r} -\color{Green}{l} + \frac{1}{2} \color{Green}{s_w} \right) + C \color{Green}{s_w} + \sum_{n=1}^N \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } + \sum_{n=1}^C \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } + \left(\color{Green}{n_C} + \color{Green}{n_E} + \color{Green}{n_D}\right) \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) + \color{Green}{n_C} \color{Green}{s_w} \right] \\ & = \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left[ \left(N + C \right) \left(\color{Green}{r} -\color{Green}{l} + \frac{1}{2} \color{Green}{s_w} \right) + \left(\color{Green}{n_C} + \color{Green}{n_E} + \color{Green}{n_D}\right) \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) + \left(C + \color{Green}{n_C} \right) \color{Green}{s_w} + \sum_{n=1}^N \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } + \sum_{n=1}^C \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } \right] \\ & = \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left[ \left(N + C + \color{Green}{n_C} + \color{Green}{n_D} + \color{Green}{n_E} \right) \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) - \color{Green}{l} \left(N + C \right) + \left(C + \color{Green}{n_C} \right) \color{Green}{s_w} + \sum_{n=1}^N \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } + \sum_{n=1}^C \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } \right] \\ & = \color{Green}{s_w} \color{Green}{s_h} 2 \pi \left[ \left(N + C + \color{Green}{n_C} + \color{Green}{n_D} + \color{Green}{n_E} \right) \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) - \color{Green}{l} \left(N + C \right) + \left(C + \color{Green}{n_C} \right) \color{Green}{s_w} + 2 \sum_{n=1}^C \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } + \sum_{n=C+1}^N \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } \right] \end{align} }
Mortero —tierra (arcilla más arenas y gravas) más estabilizante—
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_{mortero} = V_{tubo} = V_{tierra} + V_{estabilizante} = V_{tierra} + p_{estabilizante} \times V_{tierra} = (1 + p_{estabilizante}) \times V_{tierra}} Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_{tierra} = \dfrac{V_{tubo}}{1 + p_{estabilizante}}}
Tierra: arcilla más arenas y gravas
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle p_{arcilla}} – proporción de arcilla de la tierra
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle p_{arenas+gravas}} – proporción de arenas y gravas de la tierra
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_{tierra} = V_{arcilla} + V_{arenas+gravas} = p_{arcilla} \times V_{tierra} + p_{arenas+gravas} \times V_{tierra}} Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_{tierra} = (p_{arcilla} + p_{arenas+gravas}) \times V_{tierra}} Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle p_{arcilla} = 1 - p_{arenas+gravas}}
Estabilizante
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle p_{estabilizante}} – proporción de estabilizante con respecto al volumen de tierra
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_{estabilizante} = p_{estabilizante} \times V_{tierra}}
Agua
El volumen de agua necesario se calcula en función del volumen de mortero, pero no se tiene en cuenta en la suma de volúmenes que intervienen en el resultado final:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle p_{agua}}
– proporción de agua para amasar el mortero
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_{agua} = p_{agua} \times V_{mortero} = p_{agua} \times V_{tubo}}