Diferencia entre revisiones de «Cálculo de materiales»

De Terrawiki
Ir a la navegación Ir a la búsqueda
← Edición anterior
VisualWikitexto
 
(No se muestran 24 ediciones intermedias del mismo usuario)
Línea 3: Línea 3:
Al calcular el volumen de superadobe se obtienen las longitudes necesarias de saco y alambre, y el volumen de material de drenaje.
Al calcular el volumen de superadobe se obtienen las longitudes necesarias de saco y alambre, y el volumen de material de drenaje.


Para el cálculo del volumen de superadobe, se calcula la longitud de cada hilada —longitud de la circunferencia que describe el tubo— en el punto medio del saco —por similitud con el cálculo del volumen de un toro— y se multiplica por la sección del saco lleno y compactado. En cada hilada, la longitud de la circunferencia es función del radio del domo a la altura del saco.
Para el cálculo del volumen de superadobe, se calcula la longitud de cada hilada —longitud de la circunferencia que describe el tubo— en el punto medio del saco —por similitud con el cálculo del volumen de un toro— y se multiplica por el [[#Área de la sección del_saco|área de la sección del saco lleno y compactado]]. En cada hilada, la longitud de la circunferencia es función del radio del domo a la altura del saco.


[[Archivo:esquema cálculos volúmenes.png|center|1280px]]
[[Archivo:esquema cálculos volúmenes.png|center|1280px]]
Línea 13: Línea 13:
r_C = {\color{Green}{r} + {3 \over 2} \color{Green}{s_w}} \text{ — para el volumen de C}
r_C = {\color{Green}{r} + {3 \over 2} \color{Green}{s_w}} \text{ — para el volumen de C}


\\
</math>
 
<math>


r_{D,E} = {\color{Green}{r} + {1 \over 2} \color{Green}{s_w}} \text{ — para los volúmenes de D y E}
r_{D,E} = {\color{Green}{r} + {1 \over 2} \color{Green}{s_w}} \text{ — para los volúmenes de D y E}
Línea 19: Línea 21:
</math>
</math>


 
Por encima de la línea de surgencia, el radio <math>r_n</math> de la n-ésima hilada lo determinan la longitud del compás de altura <math>l</math> y la altura donde se encuentra el saco, <math>h_n</math>, que, considerando la altura hasta la mitad del saco, es igual a <math>n - {1 \over 2}</math> veces la altura del saco lleno <math>s_h</math>. Aplicando el teorema de Pitágoras:
Por encima de la línea de surgencia, el radio <math>r_n</math> de la n-ésima hilada lo determinan la longitud del compás de altura <math>l</math> y la altura donde se encuentra el saco, <math>h_n</math>, que, considerando la altura hasta la mitad del saco, es igual a <math>n − {1 \over 2}</math> veces la altura del saco lleno <math>s_h</math>. Aplicando el teorema de Pitágoras:
 


<math>
<math>
Línea 28: Línea 28:


</math>
</math>


<math>
<math>


\color{Green}{l}^2 = h_n^2 + l_n^2
l_n = \color{Green}{l} - \color{Green}{r} + r_n


\\
</math>


l_n = \color{Green}{l} - \color{Green}{r} + r_n
<math>
 
\\


h_n = \left(n - {1 \over 2} \right)\color{Green}{s_h}
h_n = \left(n - {1 \over 2} \right)\color{Green}{s_h}


</math>
</math>


<math>
<math>
Línea 49: Línea 45:
\color{Green}{l}^2 = \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2 + \left(\color{Green}{l} -\color{Green}{r} + r_n \right)^2
\color{Green}{l}^2 = \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2 + \left(\color{Green}{l} -\color{Green}{r} + r_n \right)^2


\\
</math>
 
<math>


\color{Green}{l} -\color{Green}{r} + r_n = \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2}
\color{Green}{l} -\color{Green}{r} + r_n = \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2}


\\
</math>
 
<math>


r_n = \color{Green}{r} - \color{Green}{l} + \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2}
r_n = \color{Green}{r} - \color{Green}{l} + \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2}


</math>
</math>


Añadiendo la mitad de la anchura del saco lleno, el radio resultante para el cálculo de los volúmenes del muro del domo por encima de la línea de surgencia (volúmenes en A) es:
Añadiendo la mitad de la anchura del saco lleno, el radio resultante para el cálculo de los volúmenes del muro del domo por encima de la línea de surgencia (volúmenes en A) es:


<math>
<math>
Línea 68: Línea 66:


</math>
</math>


Los volúmenes de B se calculan añadiendo a la fórmula anterior la anchura del saco lleno:
Los volúmenes de B se calculan añadiendo a la fórmula anterior la anchura del saco lleno:


<math>
<math>
Línea 79: Línea 75:
</math>
</math>


=== Área de la sección del saco ===
[[Reglas_de_diseño#Anchura de los sacos|Literatura y datos empíricos]] proporcionan información sobre la anchura y altura final del saco una vez lleno y compactado, pero no del área de la sección del saco: la forma de la sección condiciona el área, y esta el volumen resultante.


Con las fórmulas anteriores, la suma de volúmenes queda como sigue:
La forma real del saco lleno y compactado tiene los laterales aproximadamente en forma de segmento circular. Por facilidad de cálculo se puede considerar que los laterales son semicírculos, aunque el área de la sección es menor y por lo tanto también el volumen calculado, lo cual puede suponer un defecto de material. Considerando la sección del saco como un rectángulo en el que quedarían inscritas las dos secciones anteriores, se facilitan los cálculos y se añade a los mismos un exceso de material que conviene tener en cuenta como parte de la merma de material. Además, de acuerdo con los [[Reglas_de_diseño#Anchura de los sacos|datos anteriores]], se puede considerar que la altura final del saco es aproximadamente el 27,50 % de la anchura del saco vacío:


[[Archivo: secciones saco.png|center]]


<math>V = \sum_{x=A}^{E} V_x = V_A + V_B + V_C + V_C + V_E</math>
<math>
\color{Green}{L_v} \text{— anchura del saco vacío}
</math>


==== <math>V_A</math> volumen de superadobe por encima de la línea de surgencia ====
<math>
s_h \approx 0,275 \times \color{Green}{L_v} \text{— altura del saco lleno y compactado}
</math>
<math>
s_w \approx 0,725 \times \color{Green}{L_v} \text{— anchura del saco lleno y compactado}
</math>


<math>
A_{saco} = s_h \times s_w = 0,275 \times \color{Green}{L_v} \times 0,725 \times \color{Green}{L_v} \approx 0,2 \times \color{Green}{L_v}^2
</math>
=== <math>V_A</math> volumen de superadobe por encima de la línea de surgencia ===


<math>N \text{ — número de hiladas por encima de la línea de surgencia}</math>
<math>N \text{ — número de hiladas por encima de la línea de surgencia}</math>
Línea 93: Línea 103:


\color{Green}{l}^2 = h^2+(\color{Green}{l}-\color{Green}{r})^2
\color{Green}{l}^2 = h^2+(\color{Green}{l}-\color{Green}{r})^2
</math>


\\
<math>


h=\sqrt{\color{Green}{l}^2 - \left(\color{Green}{l} - \color{Green}{r} \right)^2}
h=\sqrt{\color{Green}{l}^2 - \left(\color{Green}{l} - \color{Green}{r} \right)^2}
</math>


\\
<math>


N = \dfrac{h}{\color{Green}{s_h}}
N = \dfrac{h}{\color{Green}{s_h}}
</math>


\\
<math>


N = \dfrac{
N = \dfrac{
Línea 129: Línea 142:
</math>
</math>


==== <math>V_B</math> volumen de superadobe en el contrafuerte por encima de la línea de surgencia ====
=== <math>V_B</math> volumen de superadobe en el contrafuerte por encima de la línea de surgencia ===
<math>
\color{Green}{h_c} \text{ — altura del contrafuerte por encima de la línea de surgencia (m)}
</math>
 
<math>
C \text{ — número de hiladas del contrafuerte por encima de la línea de surgencia}
</math>
 
<math>
<math>
\color{Green}{h_c} \text{ — altura del contrafuerte por encima de la línea de surgencia (m)} \\
C \text{ — número de hiladas del contrafuerte por encima de la línea de surgencia} \\
C = \dfrac{\color{Green}{h_c}}{\color{Green}{s_h}}
C = \dfrac{\color{Green}{h_c}}{\color{Green}{s_h}}
</math>
</math>
Línea 150: Línea 169:
</math>
</math>


==== <math>V_C</math> volumen de superadobe en el contrafuerte por debajo de la línea de surgencia ====
=== <math>V_C</math> volumen de superadobe en el contrafuerte por debajo de la línea de surgencia ===
<math>\color{Green}{n_C} \text{ — número de hiladas hasta la línea de surgencia del contrafuerte}</math>
<math>\color{Green}{n_C} \text{ — número de hiladas hasta la línea de surgencia del contrafuerte}</math>


Línea 160: Línea 179:
</math>
</math>


==== <math>V_D</math> volumen de superadobe por debajo de la línea de surgencia ====
=== <math>V_D</math> volumen de superadobe por debajo de la línea de surgencia ===
<math>\color{Green}{n_D} \text{ — número de hiladas hasta la línea de surgencia}</math>
<math>\color{Green}{n_D} \text{ — número de hiladas hasta la línea de surgencia}</math>


Línea 170: Línea 189:
</math>
</math>


==== <math>V_E</math> volumen de superadobe en los cimientos ====
=== <math>V_E</math> volumen de superadobe en los cimientos ===
<math>\color{Green}{n_E} \text{ — número de hiladas en los cimientos}</math>
<math>\color{Green}{n_E} \text{ — número de hiladas en los cimientos}</math>


Línea 180: Línea 199:
</math>
</math>


==== Volumen total ====
=== Volumen total ===


<math>
<math>
Línea 186: Línea 205:
\begin{align}
\begin{align}


V & = A_{saco} \times 2 \pi \left[ N \left(\color{Green}{r} - \color{Green}{l} + \frac{1}{2}\color{Green}{s_w} \right) + \sum_{n=1}^N \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2} \right]
V & = \sum_{x=A}^{E} V_x = V_A + V_B + V_C + V_C + V_E
\\
& = A_{saco} \times 2 \pi \left[ N \left(\color{Green}{r} - \color{Green}{l} + \frac{1}{2}\color{Green}{s_w} \right) + \sum_{n=1}^N \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2} \right]
\\
\\
& + A_{saco} \times 2 \pi \left[ C \left(\color{Green}{r} - \color{Green}{l} \frac{3}{2}\color{Green}{s_w} \right) + \sum_{n=1}^C \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right]
& + A_{saco} \times 2 \pi \left[ C \left(\color{Green}{r} - \color{Green}{l} \frac{3}{2}\color{Green}{s_w} \right) + \sum_{n=1}^C \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right]
Línea 347: Línea 368:
     }
     }


\right]
\right] \\
& = 0,2 \times \color{Green}{L_v}^2 \times 2 \pi


\end{align}
\left[


</math>
  \left(N + C + \color{Green}{n_C} + \color{Green}{n_D} + \color{Green}{n_E} \right)


== Área de la sección del saco ==
  \left(\color{Green}{r} + \frac{1}{2} \times 0,725 \color{Green}{L_v} \right)
[[Reglas_de_diseño#Anchura de los sacos|Literatura y datos empíricos]] proporcionan información sobre la anchura y altura final del saco una vez lleno y compactado, pero no del área de la sección del saco: la forma de la sección condiciona el área, y esta el volumen resultante.


La forma real del saco lleno y compactado tiene los laterales aproximadamente en forma de segmento circular. Por facilidad de cálculo se puede considerar que los laterales son semicírculos, aunque el área de la sección es menor y por lo tanto también el volumen calculado, lo cual puede suponer un defecto de material. Considerando la sección del saco como un rectángulo en el que quedarían inscritas las dos secciones anteriores, se facilitan los cálculos y se añade a los mismos un exceso de material que conviene tener en cuenta como parte de la merma de material. Además, de acuerdo con los [[Reglas_de_diseño#Anchura de los sacos|datos anteriores]], se puede considerar que la altura final del saco es aproximadamente el 27,50 % de la anchura del saco vacío:
  - \color{Green}{l} \left(N + C \right)


[[Archivo: secciones saco.png|center]]
  + \left(C + \color{Green}{n_C} \right) \times 0,725 \color{Green}{L_v}


  + 2 \sum_{n=1}^C \sqrt{


<math>
    \color{Green}{l}^2 -
\color{Green}{L_v} \text{— anchura del saco vacío} \\
s_h = 0,275 \times \color{Green}{L_v} \text{— altura del saco lleno y compactado} \\
s_w = 0,725 \times \color{Green}{L_v} \text{— anchura del saco lleno y compactado}
</math>


===== Sección rectangular =====
    \left[


[[Archivo:sección_saco_rectangular.png|none|frame|Sección rectangular]]
      \left(n - \frac{1}{2} \right) \times 0,275 \color{Green}{L_v}


<math>
    \right]^2
s_w = \color{Green}{L_v} - \color{Green}{s_h}
\\
A_{saco} = s_w \times \color{Green}{s_h} = \left(\color{Green}{L_v} - \color{Green}{s_h} \right) \times \color{Green}{s_h}</math>


===== Sección con laterales semicurculares =====
    }


[[Archivo:sección_saco_arco.png|thumb|Sección con laterales como segmentos circulares]]
  + \sum_{n=C+1}^N \sqrt{


Aunque en realidad los lados la sección del saco son sectores circulares, para añadir un margen de seguridad conveniente en los cálculos se considera la sección con los laterales semicurculares:
    \color{Green}{l}^2 -


[[Archivo:sección_saco_semicírculo.png|none|frame|Sección con laterales semicirculares]]
    \left[
 
<math>
s_w = \color{Green}{L_v} - \dfrac{\pi \color{Green}{s_h}}{2} + \color{Green}{s_h} = \color{Green}{L_v} + \color{Green}{s_h}\left(1 - \dfrac{\pi}{2}\right)
\\
A_{saco} = \left(\color{Green}{L_v} - \dfrac{\pi \color{Green}{s_h}}{2} \right) \times \color{Green}{s_h} + \pi \left(\dfrac{\color{Green}{s_h}}{2}\right)^2 = \color{Green}{L_v} \color{Green}{s_h} - \dfrac{\pi \color{Green}{s_h}^2}{4}
</math>


===== Sección con laterales como segmentos circulares =====
      \left(n - \frac{1}{2} \right) \times 0,275 \color{Green}{L_v}


[[Archivo:sección_saco_arco.png|none|frame|Sección con laterales como segmentos circulares]]
    \right]^2


<math>
    }
s_w = \color{Green}{L_v} - \dfrac{\pi \color{Green}{s_h}}{3} + 2 \left(\color{Green}{s_h} - \sqrt{\color{Green}{s_h}^2 - \left(\dfrac{\color{Green}{s_h}}{2} \right)^2} \right)
= \color{Green}{L_v} - \dfrac{\pi \color{Green}{s_h}}{3} + 2 \left(\color{Green}{s_h} - \color{Green}{s_h} \dfrac{\sqrt{3}}{2} \right)
= \color{Green}{L_v} + \color{Green}{s_h} \left( 2 - \dfrac{\sqrt{3}}{2} - \dfrac{\pi}{3} \right)
= \color{Green}{L_v} + \dfrac{\color{Green}{s_h}}{3} \left( 6 - 3\sqrt{3} - {\pi} \right)


\right]


\\


\sin \alpha = \dfrac{\dfrac{\color{Green}{s_h}}{2}}{\color{Green}{s_h}} = \dfrac{1}{2}; \alpha = 30^\circ
\\
\begin{align}
A_{saco} & = \left(\color{Green}{L_v} - \dfrac{\pi \color{Green}{s_h}}{3} \right) \times \color{Green}{s_h} + 2 \left(\pi \color{Green}{s_h}^2 \times \dfrac{2\alpha}{360} - \dfrac{1}{2} \times \color{Green}{s_h} \sqrt{\color{Green}{s_h}^2 - \left(\dfrac{\color{Green}{s_h}}{2} \right)^2} \right) \\
& = \color{Green}{L_v} \color{Green}{s_h} - \dfrac{\pi \color{Green}{s_h}^2}{3} + 2 \left(\pi \color{Green}{s_h}^2 \times \dfrac{1}{6} - \dfrac{1}{2} \times \dfrac{\color{Green}{s_h}^2 \sqrt{3}}{2} \right) \\
& = \color{Green}{L_v} \color{Green}{s_h} - \dfrac{\pi \color{Green}{s_h}^2}{3} + \dfrac{\pi \color{Green}{s_h}^2}{3} - \dfrac{\color{Green}{s_h}^2 \sqrt{3}}{2} \\
& = \color{Green}{L_v} \color{Green}{s_h} - \color{Green}{s_h}^2 \dfrac{\sqrt{3}}{2}
\end{align}
\end{align}
</math>
==== Sección para cálculos ====
Usar una sección u otra conlleva variaciones en los cálculos, ya que el área de cada una es distinta:
{| class="wikitable"
|-
!  !!  !! colspan="9" | Altura del saco lleno y compactado
|-
!  !!  !! colspan="3" | Sección rectangular !! colspan="3" | Sección con semicírculos !! colspan="3" | Sección con segmentos circulares
|-
|  || in || 2,00 || 3,00 || 5,00 || 2,00 || 3,00 || 5,00 || 2,00 || 3,00 || 5,00
|-
|  || cm || 5,08 || 7,62 || 12,70 || 5,08 || 7,62 || 12,70 || 5,08 || 7,62 || 12,70
|-
| rowspan="7" | Anchura del saco vacío (cm) || 30||126,59||170,54||219,71||132,13||183,00||254,32||130,05||178,31||241,32
|-
| 35||151,99||208,64||283,21||157,53||221,10||317,82||155,45||216,41||304,82
|-
| 40||177,39||246,74||346,71||182,93||259,20||381,32||180,85||254,51||368,32
|-
| 45||202,79||284,84||410,21||208,33||297,30||444,82||206,25||292,61||431,82
|-
| 50||228,19||322,94||473,71||233,73||335,40||508,32||231,65||330,71||495,32
|-
| 55||253,59||361,04||537,21||259,13||373,50||571,82||257,05||368,81||558,82
|-
| 60 ||278,99||399,14||600,71||284,53||411,60||635,32||282,45||406,91||622,32
|}
==== Valores de sección ====
El área de la sección del saco, <math>A_{saco}</math>, debe multiplicarse por la longitud del mismo —longitud de la circunferencia que describe el tubo en la hilada correspondiente—, que en cada caso es función del radio del domo a la altura del saco; a esta medida se suma la mitad de la anchura del saco lleno —por similitud con el cálculo del volumen de un toro—. Por debajo de la línea de surgencia el radio es constante:
<math>
r_C = {\color{Green}{r} + {3 \over 2} s_w} \text{ — para el volumen de C}
\\
r_{D,E} = {\color{Green}{r} + {1 \over 2} s_w} \text{ — para los volúmenes de D y E}
</math>
Por encima de la línea de surgencia, el radio <math>r_n</math> de la n-ésima hilada lo determinan la longitud del compás de altura <math>l</math> y la altura donde se encuentra el saco, <math>h_n</math>, que, considerando la altura hasta la mitad del saco, es igual a <math>n − {1 \over 2}</math> veces la altura del saco lleno <math>s_h</math>. Aplicando el teorema de Pitágoras:
<math>
\color{Green}{l}^2 = h_n^2 + l_n^2
</math>
<math>
\color{Green}{l}^2 = h_n^2 + l_n^2
\\
l_n = \color{Green}{l} - \color{Green}{r} + r_n
\\
h_n = \left(n - {1 \over 2} \right)\color{Green}{s_h}
</math>
<math>
\color{Green}{l}^2 = \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2 + \left(\color{Green}{l} -\color{Green}{r} + r_n \right)^2
\\
\color{Green}{l} -\color{Green}{r} + r_n = \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2}
\\
r_n = \color{Green}{r} - \color{Green}{l} + \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2}


</math>
</math>
Añadiendo la mitad de la anchura del saco lleno, el radio resultante para el cálculo de los volúmenes del muro del domo por encima de la línea de surgencia (volúmenes en A) es:
<math>
r_{n(A)} = \color{Green}{r} - \color{Green}{l} + {1 \over 2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2}
</math>
Los volúmenes de B se calculan añadiendo a la fórmula anterior la anchura del saco lleno:
<math>
r_{n(B)} = \color{Green}{r} - \color{Green}{l} + {3 \over 2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2}
</math>
Con las fórmulas anteriores, la suma de volúmenes queda como sigue:
<math>V = \sum_{x=A}^{E} V_x = V_A + V_B + V_C + V_C + V_E</math>
== Mortero —tierra (arcilla más arenas y gravas) más estabilizante—==
<math>V_{mortero} = V_{tubo} = V_{tierra} + V_{estabilizante} = V_{tierra} + p_{estabilizante} \times V_{tierra} = (1 + p_{estabilizante}) \times V_{tierra}</math>
<math>V_{tierra} = \dfrac{V_{tubo}}{1 + p_{estabilizante}}</math>
== Tierra: arcilla más arenas y gravas ==
<math>p_{arcilla}</math>  – proporción de arcilla de la tierra
<math>p_{arenas+gravas}</math> – proporción de arenas y gravas de la tierra
<math>V_{tierra} = V_{arcilla} + V_{arenas+gravas} = p_{arcilla} \times V_{tierra} + p_{arenas+gravas} \times V_{tierra}</math>
<math>V_{tierra} = (p_{arcilla} + p_{arenas+gravas}) \times V_{tierra}</math>
<math>p_{arcilla} = 1 - p_{arenas+gravas}</math>
== Estabilizante ==
<math>p_{estabilizante}</math> – proporción de estabilizante con respecto al volumen de tierra
<math>V_{estabilizante} = p_{estabilizante} \times V_{tierra}</math>
== Agua ==
El volumen de agua necesario se calcula en función del volumen de mortero, pero no se tiene en cuenta en la suma de volúmenes que intervienen en el resultado final:
<math>p_{agua}</math> – proporción de agua para amasar el mortero
<math>V_{agua} = p_{agua} \times V_{mortero} = p_{agua} \times V_{tubo}</math>

Revisión actual - 21:45 19 ago 2018

Volumen total de superadobe

Al calcular el volumen de superadobe se obtienen las longitudes necesarias de saco y alambre, y el volumen de material de drenaje.

Para el cálculo del volumen de superadobe, se calcula la longitud de cada hilada —longitud de la circunferencia que describe el tubo— en el punto medio del saco —por similitud con el cálculo del volumen de un toro— y se multiplica por el área de la sección del saco lleno y compactado. En cada hilada, la longitud de la circunferencia es función del radio del domo a la altura del saco.

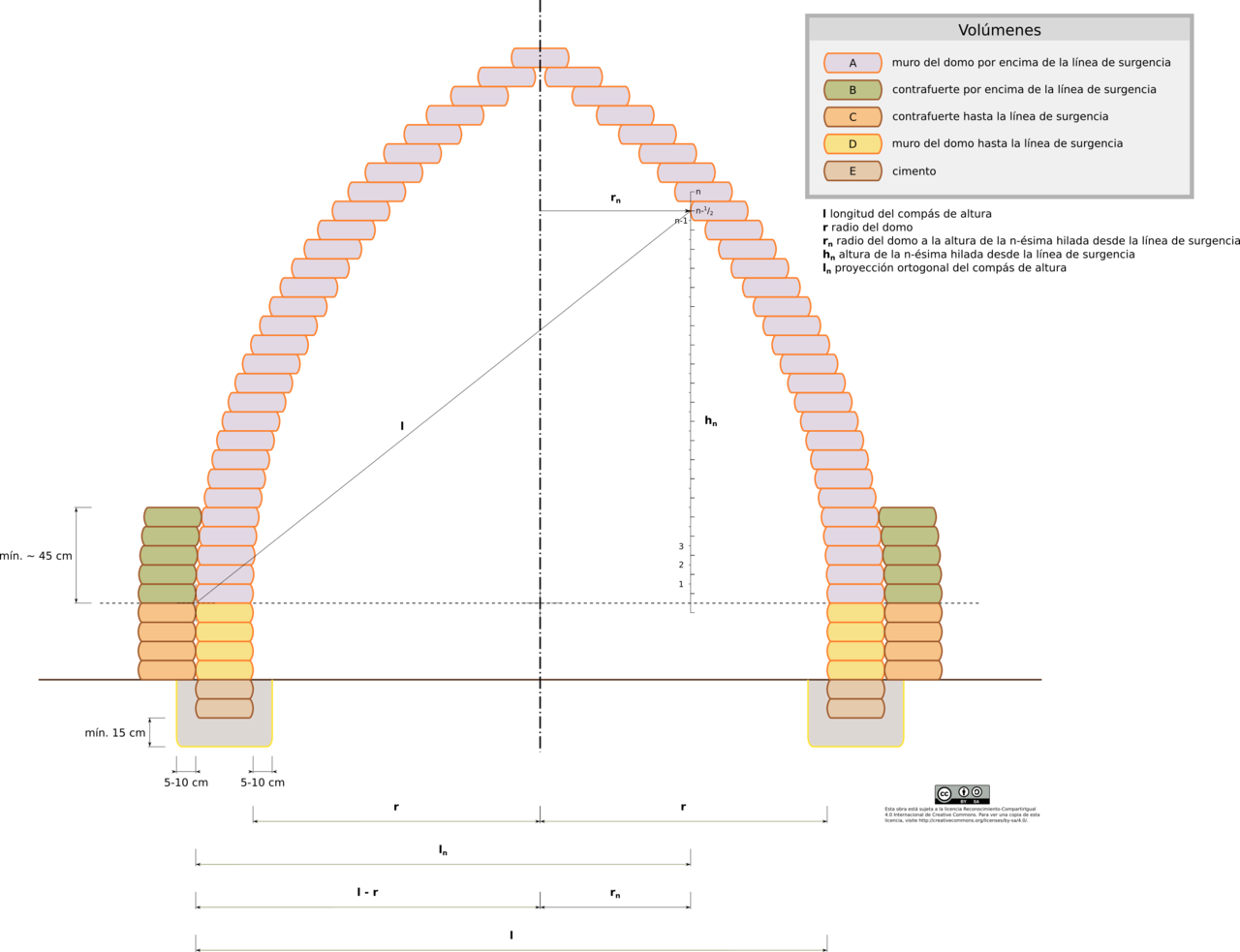
Por debajo de la línea de surgencia el radio es constante:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle r_C = {\color{Green}{r} + {3 \over 2} \color{Green}{s_w}} \text{ — para el volumen de C} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle r_{D,E} = {\color{Green}{r} + {1 \over 2} \color{Green}{s_w}} \text{ — para los volúmenes de D y E} }

Por encima de la línea de surgencia, el radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle r_n} de la n-ésima hilada lo determinan la longitud del compás de altura Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle l} y la altura donde se encuentra el saco, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle h_n} , que, considerando la altura hasta la mitad del saco, es igual a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle n - {1 \over 2}} veces la altura del saco lleno Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle s_h} . Aplicando el teorema de Pitágoras:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{l}^2 = h_n^2 + l_n^2 }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle l_n = \color{Green}{l} - \color{Green}{r} + r_n }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle h_n = \left(n - {1 \over 2} \right)\color{Green}{s_h} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{l}^2 = \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2 + \left(\color{Green}{l} -\color{Green}{r} + r_n \right)^2 }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{l} -\color{Green}{r} + r_n = \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle r_n = \color{Green}{r} - \color{Green}{l} + \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2} }

Añadiendo la mitad de la anchura del saco lleno, el radio resultante para el cálculo de los volúmenes del muro del domo por encima de la línea de surgencia (volúmenes en A) es:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle r_{n(A)} = \color{Green}{r} - \color{Green}{l} + {1 \over 2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2} }

Los volúmenes de B se calculan añadiendo a la fórmula anterior la anchura del saco lleno:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle r_{n(B)} = \color{Green}{r} - \color{Green}{l} + {3 \over 2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2 - \left[\left(n - {1 \over 2} \right)\color{Green}{s_h} \right]^2} }

Área de la sección del saco

Literatura y datos empíricos proporcionan información sobre la anchura y altura final del saco una vez lleno y compactado, pero no del área de la sección del saco: la forma de la sección condiciona el área, y esta el volumen resultante.

La forma real del saco lleno y compactado tiene los laterales aproximadamente en forma de segmento circular. Por facilidad de cálculo se puede considerar que los laterales son semicírculos, aunque el área de la sección es menor y por lo tanto también el volumen calculado, lo cual puede suponer un defecto de material. Considerando la sección del saco como un rectángulo en el que quedarían inscritas las dos secciones anteriores, se facilitan los cálculos y se añade a los mismos un exceso de material que conviene tener en cuenta como parte de la merma de material. Además, de acuerdo con los datos anteriores, se puede considerar que la altura final del saco es aproximadamente el 27,50 % de la anchura del saco vacío:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{L_v} \text{— anchura del saco vacío} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle s_h \approx 0,275 \times \color{Green}{L_v} \text{— altura del saco lleno y compactado} } Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle s_w \approx 0,725 \times \color{Green}{L_v} \text{— anchura del saco lleno y compactado} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle A_{saco} = s_h \times s_w = 0,275 \times \color{Green}{L_v} \times 0,725 \times \color{Green}{L_v} \approx 0,2 \times \color{Green}{L_v}^2 }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_A} volumen de superadobe por encima de la línea de surgencia

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle N \text{ — número de hiladas por encima de la línea de surgencia}}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{l}^2 = h^2+(\color{Green}{l}-\color{Green}{r})^2 }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle h=\sqrt{\color{Green}{l}^2 - \left(\color{Green}{l} - \color{Green}{r} \right)^2} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle N = \dfrac{h}{\color{Green}{s_h}} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle N = \dfrac{ \sqrt{ \color{Green}{l}^2 - \left(\color{Green}{l} - \color{Green}{r} \right)^2 } }{\color{Green}{s_h}} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_A(n) & = A_{saco} \times 2 \pi r_{n(A)} \\ & = A_{saco} \times 2 \pi \left(\color{Green}{r} - \color{Green}{l} + \frac{1}{2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right) \end{align} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_A & = A_{saco} \times 2 \pi \sum_{n=1}^N \left(\color{Green}{r} - \color{Green}{l} + \frac{1}{2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right) \\ & = A_{saco} \times 2 \pi \left[ N \left(\color{Green}{r} - \color{Green}{l} + \frac{1}{2}\color{Green}{s_w} \right) + \sum_{n=1}^N \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right] \end{align} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_B} volumen de superadobe en el contrafuerte por encima de la línea de surgencia

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{h_c} \text{ — altura del contrafuerte por encima de la línea de surgencia (m)} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle C \text{ — número de hiladas del contrafuerte por encima de la línea de surgencia} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle C = \dfrac{\color{Green}{h_c}}{\color{Green}{s_h}} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_B(n) & = A_{saco} \times 2 \pi r_{n(B)} \\ & = A_{saco} \times 2 \pi \left(\color{Green}{r} - \color{Green}{l} + \frac{3}{2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right) \end{align} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_B & = A_{saco} \times 2 \pi \sum_{n=1}^C \left(\color{Green}{r} - \color{Green}{l} + \frac{3}{2}\color{Green}{s_w} + \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right) \\ & = A_{saco} \times 2 \pi \left[ C \left(\color{Green}{r} - \color{Green}{l} + \frac{3}{2}\color{Green}{s_w} \right) + \sum_{n=1}^C \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right] \end{align} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_C} volumen de superadobe en el contrafuerte por debajo de la línea de surgencia

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{n_C} \text{ — número de hiladas hasta la línea de surgencia del contrafuerte}}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_C & = \color{Green}{n_c} \times A_{saco} \times(2 \pi r_c) \\ & = \color{Green}{n_c} \times A_{saco} \times 2 \pi \left(\color{Green}{r} + \frac{3}{2} \color{Green}{s_w} \right) \end{align} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_D} volumen de superadobe por debajo de la línea de surgencia

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{n_D} \text{ — número de hiladas hasta la línea de surgencia}}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_D & = \color{Green}{n_D} \times A_{saco} \times(2 \pi r_D) \\ & = \color{Green}{n_D} \times A_{saco} \times 2 \pi \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) \end{align} }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle V_E} volumen de superadobe en los cimientos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \color{Green}{n_E} \text{ — número de hiladas en los cimientos}}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V_E & = \color{Green}{n_E} \times A_{saco} \times(2 \pi r_E) \\ & = \color{Green}{n_E} \times A_{saco} \times 2 \pi \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) \end{align} }

Volumen total

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://es.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align} V & = \sum_{x=A}^{E} V_x = V_A + V_B + V_C + V_C + V_E \\ & = A_{saco} \times 2 \pi \left[ N \left(\color{Green}{r} - \color{Green}{l} + \frac{1}{2}\color{Green}{s_w} \right) + \sum_{n=1}^N \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2} \right] \\ & + A_{saco} \times 2 \pi \left[ C \left(\color{Green}{r} - \color{Green}{l} \frac{3}{2}\color{Green}{s_w} \right) + \sum_{n=1}^C \sqrt{\color{Green}{l}^2-\left[\left(n - \frac{1}{2} \right)\color{Green}{s_h} \right]^2} \right] \\ & + A_{saco} \times 2 \pi \times \color{Green}{n_C} \left(\color{Green}{r} + \frac{3}{2} \color{Green}{s_w} \right) \\ & + A_{saco} \times 2 \pi \times \color{Green}{n_D} \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) \\ & + A_{saco} \times 2 \pi \times \color{Green}{n_E} \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) \\ & = A_{saco} \times 2 \pi \left[ \left(N + C \right) \left(\color{Green}{r} -\color{Green}{l} + \frac{1}{2} \color{Green}{s_w} \right) + C \color{Green}{s_w} + \sum_{n=1}^N \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } + \sum_{n=1}^C \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } + \left(\color{Green}{n_C} + \color{Green}{n_E} + \color{Green}{n_D}\right) \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) + \color{Green}{n_C} \color{Green}{s_w} \right] \\ & = A_{saco} \times 2 \pi \left[ \left(N + C \right) \left(\color{Green}{r} -\color{Green}{l} + \frac{1}{2} \color{Green}{s_w} \right) + \left(\color{Green}{n_C} + \color{Green}{n_E} + \color{Green}{n_D}\right) \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) + \left(C + \color{Green}{n_C} \right) \color{Green}{s_w} + \sum_{n=1}^N \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } + \sum_{n=1}^C \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } \right] \\ & = A_{saco} \times 2 \pi \left[ \left(N + C + \color{Green}{n_C} + \color{Green}{n_D} + \color{Green}{n_E} \right) \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) - \color{Green}{l} \left(N + C \right) + \left(C + \color{Green}{n_C} \right) \color{Green}{s_w} + \sum_{n=1}^N \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } + \sum_{n=1}^C \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } \right] \\ & = A_{saco} \times 2 \pi \left[ \left(N + C + \color{Green}{n_C} + \color{Green}{n_D} + \color{Green}{n_E} \right) \left(\color{Green}{r} + \frac{1}{2} \color{Green}{s_w} \right) - \color{Green}{l} \left(N + C \right) + \left(C + \color{Green}{n_C} \right) \color{Green}{s_w} + 2 \sum_{n=1}^C \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } + \sum_{n=C+1}^N \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \color{Green}{s_h} \right]^2 } \right] \\ & = 0,2 \times \color{Green}{L_v}^2 \times 2 \pi \left[ \left(N + C + \color{Green}{n_C} + \color{Green}{n_D} + \color{Green}{n_E} \right) \left(\color{Green}{r} + \frac{1}{2} \times 0,725 \color{Green}{L_v} \right) - \color{Green}{l} \left(N + C \right) + \left(C + \color{Green}{n_C} \right) \times 0,725 \color{Green}{L_v} + 2 \sum_{n=1}^C \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \times 0,275 \color{Green}{L_v} \right]^2 } + \sum_{n=C+1}^N \sqrt{ \color{Green}{l}^2 - \left[ \left(n - \frac{1}{2} \right) \times 0,275 \color{Green}{L_v} \right]^2 } \right] \end{align} }

Obtenido de «https://terrawiki.es/wiki/index.php?title=Cálculo_de_materiales&oldid=2137»